Application of Vector Product¶
矢量乘法的应用¶
Left hand and right hand rule 左手法则与右手法则¶
我们知道两个向量的叉乘会得到一个新的向量,该向量与两个向量所在平面垂直
$$first \times second = last$$
但是到底垂直向上还是垂直向下,这个要做好约定,既通过左手法则或右手法则约定:
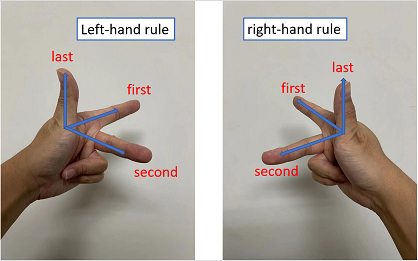
左手法则和右手法则的要点是,食指代表第一个向量的方向,中指代表第二个向量的方向,两个向量在同一个平面,但是不需要垂直,作为结果的第三个向量的方向由大拇指决定,此外:
1) 如果采用左手法则,食指到中指为顺时针旋转(从上向下观看)
2) 如果采用右手法则,食指到中指为逆时针旋转(从上向下观看)
本门课程沿用线性代数的传统,用右手法则定义叉乘后向量的方向,此外三维空间中的基向量$i$,$j$,$k$关系如下:
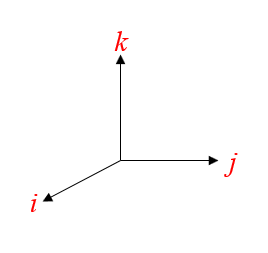
$=A_1 B_1 i \times i + A_1 B_2 i \times j + A_1 B_3 i \times k$ $+A_2 B_1 j \times i + A_2 B_2 j \times j + A_2 B_3 j \times k$
$+A_3 B_1 k \times i + A_3 B_2 k \times j + A_3 B_3 k \times k$
$=A_1 B_2 k - A_1 B_3 j -A_2 B_1 k + A_2 B_3 i +A_3 B_1 j - A_3 B_2 i$
Vector product to calculate the area 通过向量积计算面积¶
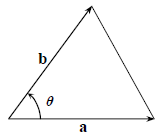
In pure mathematics, you have already met the expression "$absin\theta$" in connection with areas. The triangle area$=\|\frac{1}{2} absin\theta\| = \|\frac{1}{2} a\times b\|$
在纯数学中,您已经遇到过与面积相关的表达式“$absin\theta$”。 三角形面积$=\|\frac{1}{2} absin\theta\| = \|\frac{1}{2} a\times b\|$
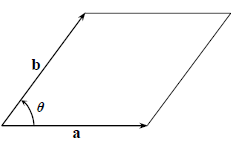
The area of a parallelogram is 平行四边形的面积是 $$\|a\times b\|$$
To find the areas of triangles or parallelograms using vector products, it is therefore necessary to first find two vectors representing adjacent edges, and the angle between them
要使用矢量积求三角形或平行四边形的面积,因此需要首先找到表示相邻边的两个矢量,以及它们之间的角度.
Example
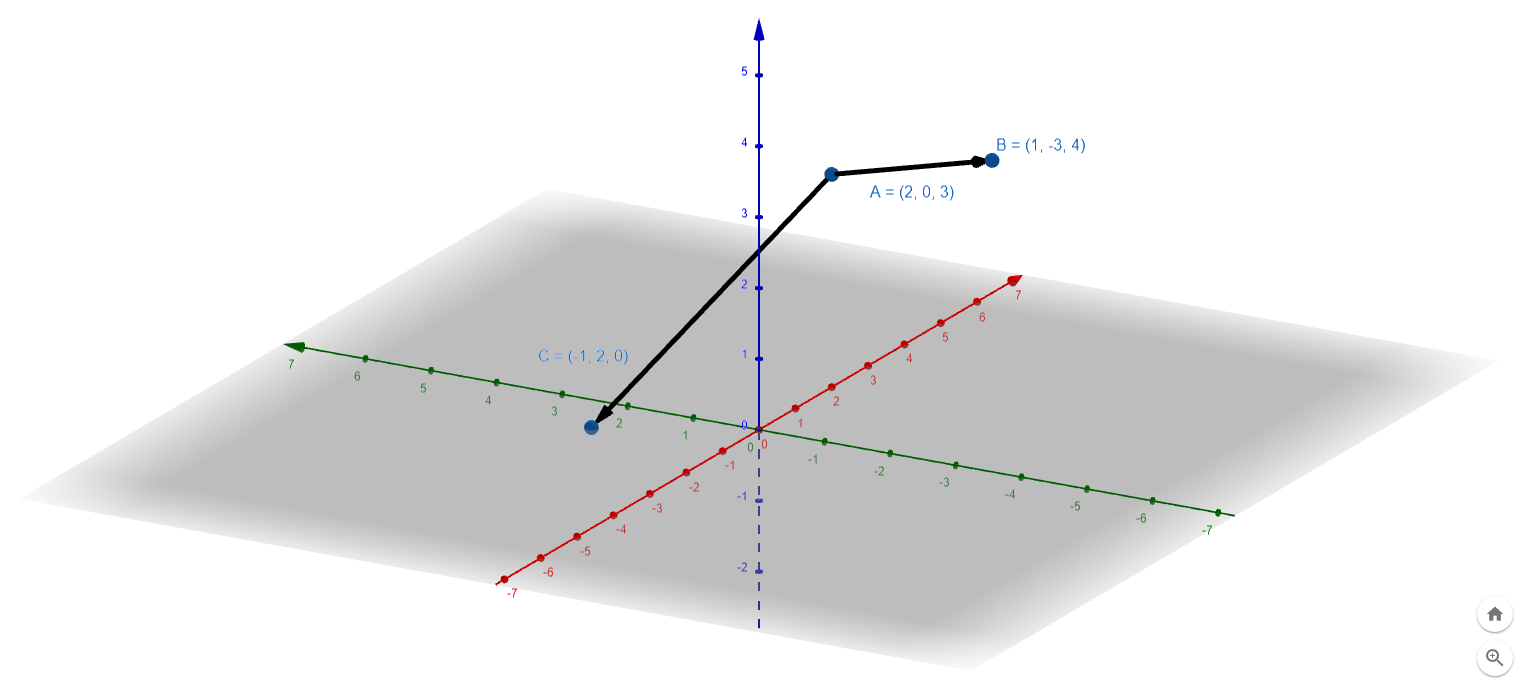
Find the area of triangle ABC in 3 dimensional space, where A is (2, 0, 3), B is (1, −3, 4) and C is (−1, 2, 0)
计算3维空间中三角形ABC的面积,这里的A坐标是(2, 0, 3), B 坐标是 (1, −3, 4) C 坐标是 (−1, 2, 0)
Exercise
There is parallelogram ABCD in 3 dimensional space, where A is (1, 1, 3), B is (2, 3, 3) and C is (3, 1, 3)
3维空间中有一个平行四边形ABCD,A坐标是(1, 1, 3), B 坐标是 (2, 3, 3) C 坐标是 (3, 1, 3)
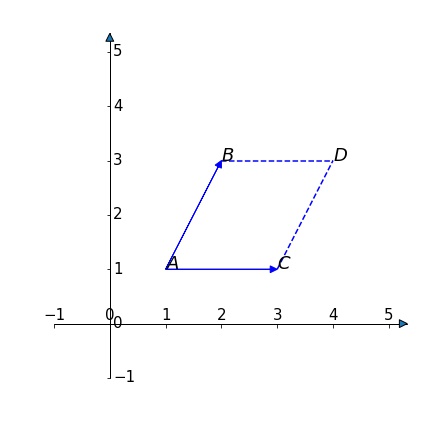 1) Find the area of ABCD 计算ABCD的面积
1) Find the area of ABCD 计算ABCD的面积
2) Get the coordinate of D 找到D点的坐标
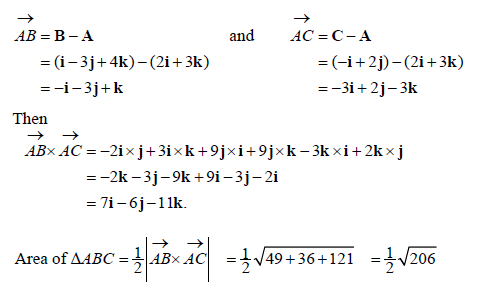
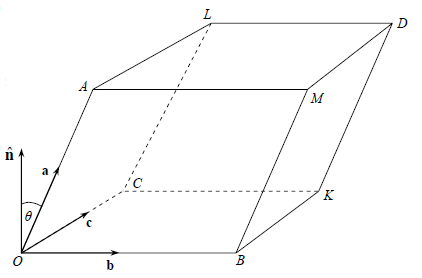
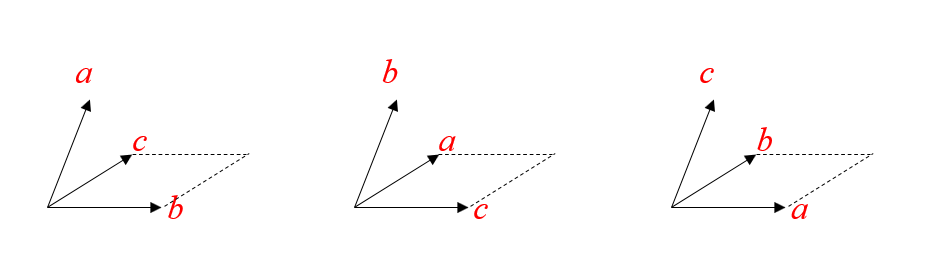 You should note that these equal triple products all involve the same cyclic order of the three vectors, i.e.
You should note that these equal triple products all involve the same cyclic order of the three vectors, i.e.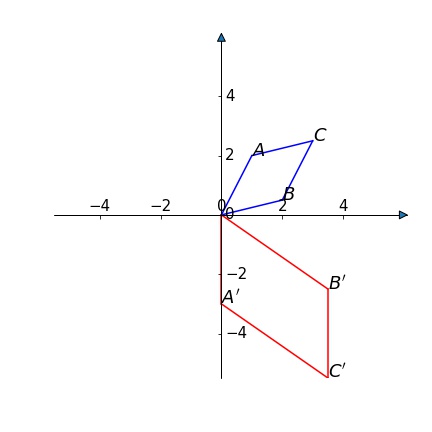
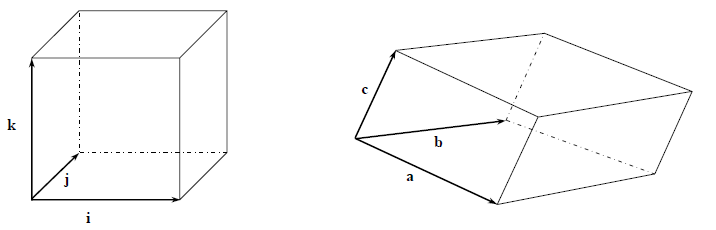 它的三条楞刚好是单位基矢量$i$,$j$,$k$,如果用矩阵表示是
$i=\left[\begin{array}{c}1\\0\\0\end{array}\right]$, $j=\left[\begin{array}{c}0\\1\\0\end{array}\right]$,$k=\left[\begin{array}{c}0\\0\\1\end{array}\right]$
它的三条楞刚好是单位基矢量$i$,$j$,$k$,如果用矩阵表示是
$i=\left[\begin{array}{c}1\\0\\0\end{array}\right]$, $j=\left[\begin{array}{c}0\\1\\0\end{array}\right]$,$k=\left[\begin{array}{c}0\\0\\1\end{array}\right]$