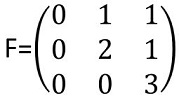项目式学习：行最简矩阵

1 Priciples 原理

1.1 Row Echelon Form 行阶梯形矩阵

A matrix is said to be in row echelon [ˈeʃəlɒn] form if it satisfies the following two conditions:
满足以下条件的矩阵称为行阶梯形矩阵
(a) All zero rows are gathered near the bottom.
全为零的行位于矩阵下方
(b) The first nonzero entry of a row, called the leading entry (also names pivot) of that row, is ahead of the first nonzero entry of the next row.
每个非零行的首个非零元所在列下方全为零 (首个非零元叫做每一行的主元)

These are row echelon matrix
以下是阶梯型矩阵

These are not row echelon matrix
以下不是阶梯型矩阵

Explain: Matrix D: all zero rows are not on the bottom
全零行不在矩阵最下方
Matrix E: The leading entry (also names pivot) of row 2, is NOT ahead of the leading entry of the row 3.
第二行的主元下方的元素不是0，换句话说就是第二行的主元没有领先于第三行的主元
Matrix F: The leading entry (also names pivot) of row 1, is NOT ahead of the leading entry of the row 2.
第一行的主元下方的元素不是0，换句话说就是第一行的主元没有领先于第二行的主元

1.2 Reduced Row Echelon Form 行最简矩阵

A matrix in row echelon form is said to be in reduced row echelon form if it satisfies two more conditions:
满足如下两个条件的行阶梯型矩阵成为行最简矩阵
(c) The leading entry of every nonzero row is 1.
每个非零行的主元都为1
(d) Each leading entry 1 is the only nonzero entry in its column.
主元所在列其它元素均为0

Example: row echelon vs reduced row echelon B change to reduced row echelon matrix R if:
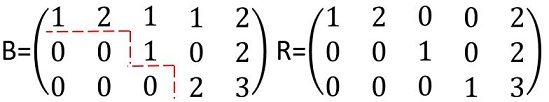
阶梯矩阵B变成行最简矩阵R，如果：
1) change B(3,4) from 2 to 1 (leading entry is 1)
将B(3,4)从2变成1 （以实现主元为1的要求）
2) change B(1,3) from 1 to 0 (leading entry in B(2,3) must be the only nonzero element in its column)
将B(1,3)从1变成0 （主元为所在列唯一的非零元素）
3) change B(1,4) from 1 to 0 (leading entry in B(3,4) must be the only nonzero element in its column)
将B(1,4)从1变成0 （主元为所在列唯一的非零元素）

2. Project & Demo 项目演练

Getting RREF by Elementary Row Transform
通过初等行变换获得行最简矩阵
要求：每执行一次初等行变换，观察以下变换前后的不同，自我总结变换的思路

首先定义以下代码

def row_times_number(matrix,row,number):
    import copy
    matrix_new = matrix.copy()
    matrix_new[row-1]=matrix.copy()[row-1]*number
    return matrix_new
def add_row_to_row(matrix,add_row,to_row,by):
    matrix_new = matrix.copy()
    matrix_new[to_row-1]=matrix.copy()[to_row-1]+matrix.copy()[add_row-1]*by
    return matrix_new
def switch_row(matrix,row_a,row_b):
    matrix_new =matrix.copy()
    matrix_new[row_a-1]=matrix.copy()[row_b-1]
    matrix_new[row_b-1]=matrix.copy()[row_a-1]
    return matrix_new

$$ A_{0}=\left[\begin{array}{ccccc}0&0&2&1&0\\0&1&1&-2&1\\0&1&0&2&0\\0&2&-2&1&1 \end{array}\right]$$

定义$A_0$

import numpy as np
A0 = np.array([[0,0,2,1,0],[0,1,1,-2,1],[0,1,0,2,0],[0,2,-2,1,1]]).astype('float64')
np.around(A0,6)

array([[ 0.,  0.,  2.,  1.,  0.],
       [ 0.,  1.,  1., -2.,  1.],
       [ 0.,  1.,  0.,  2.,  0.],
       [ 0.,  2., -2.,  1.,  1.]])

获得$A_1$: row1 与 row 4 交换

A1 = switch_row(A0,1,4)

A1

获得$A_2$: row1 乘以-1/2 加到 row2

A2 = add_row_to_row(A1,1,2,-1/2)
A2 

获得$A_3$: row1 乘以-1/2 加到 row3

A3 = add_row_to_row(A2,1,3,-1/2)
A3 

获得$A_4$: row1 乘以1/2

A4 = row_times_number(A3,1,1/2)
A4

获得$A_5$: row2 乘以-1/2 加到 row3

A5 = add_row_to_row(A4,2,3,-1/2)
A5

获得$A_6$: row2 乘以-1 加到 row4

A6 = add_row_to_row(A5,2,4,-1)
A6

获得$A_7$: row2 乘以1/2 加到 row1

A7 = add_row_to_row(A6,2,1,1/2)
A7

获得$A_8$: row2 乘以1/2

A8 = row_times_number(A7,2,1/2)
A8

获得$A_9$: row3 乘以-3.5/2.75 加到 row4

A9 = add_row_to_row(A8,3,4,-3.5/2.75)
np.around(A9,6)

获得$A_{10}$: row3 乘以0.75/2.75 加到 row1

A10 = add_row_to_row(A9,3,1,0.75/2.75)
np.around(A10,6)

获得$A_{11}$: row3 乘以1.25/2.75 加到 row2

A11 = add_row_to_row(A10,3,2,1.25/2.75)
np.around(A11,6)

获得$A_{12}$: row3 乘以1/2.75

A12 = row_times_number(A11,3,1/2.75)
np.around(A12,6)

获得$A_{13}$: row4 乘以-6/5 加到 row1

A13 = add_row_to_row(A12,4,1,-6/5)
np.around(A13,6)

获得$A_{14}$: row4 乘以1/5 加到 row2

A14 = add_row_to_row(A13,4,2,1/5)
np.around(A14,6)

获得$A_{15}$: row4 乘以3/5 加到 row3

A15 = add_row_to_row(A14,4,3,3/5)
np.around(A15,6)

获得$A_{16}$: row4 乘以11/5

A16 = row_times_number(A15,4,11/5)
np.around(A16,6)

请自行总结规律

3.Implication 实战

采用以上方法计算以下矩阵的行最简矩阵 $$ A_{0}=\left[\begin{array}{cc}1&2\\3&4 \end{array}\right]$$

$$ A_{0}=\left[\begin{array}{cccc}1&2&3&4\\5&6&7&8\\9&0&1&2 \end{array}\right]$$$$ A_{0}=\left[\begin{array}{ccccc}1&1&0&-3&-1\\1&-1&2&-1&0\\4&-2&6&3&-4\\2&4&-2&4&-7 \end{array}\right]$$